In geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues.
The Desargues configuration can be constructed in two dimensions from the points and lines occurring in Desargues's theorem, in three dimensions from five planes in general position, or in four dimensions from the 5-cell, the four-dimensional regular simplex. It has a large group of symmetries, taking any point to any other point and any line to any other line. It is also self-dual, meaning that if the points are replaced by lines and vice versa using projective duality, the same configuration results.
Graphs associated with the Desargues configuration include the Desargues graph (its graph of point-line incidences) and the Petersen graph (its graph of non-incident lines). The Desargues configuration is one of ten different configurations with ten points and lines, three points per line, and three lines per point, nine of which can be realized in the Euclidean plane.
Constructions edit
Two dimensions edit
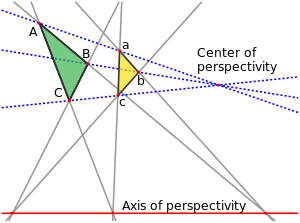
Two triangles and are said to be in perspective centrally if the lines , , and meet in a common point, called the center of perspectivity. They are in perspective axially if the intersection points of the corresponding triangle sides, , , and all lie on a common line, the axis of perspectivity. Desargues's theorem in geometry states that these two conditions are equivalent: if two triangles are in perspective centrally then they must also be in perspective axially, and vice versa. When this happens, the ten points and ten lines of the two perspectivities (the six triangle vertices, three crossing points, and center of perspectivity, and the six triangle sides, three lines through corresponding pairs of vertices, and axis of perspectivity) together form an instance of the Desargues configuration.[1]
Three dimensions edit
Although it may be embedded in two dimensions, the Desargues configuration has a very simple construction in three dimensions: for any configuration of five planes in general position in Euclidean space, the ten points where three planes meet and the ten lines formed by the intersection of two of the planes together form an instance of the configuration.[2] This construction is closely related to the property that every projective plane that can be embedded into a 3-dimensional projective space obeys Desargues' theorem. This three-dimensional realization of the Desargues configuration is also called the complete pentahedron.[2]
Four dimensions edit
The 5-cell or pentatope (a regular simplex in four dimensions) has five vertices, ten edges, ten triangular ridges (2-dimensional faces), and five tetrahedral facets; the edges and ridges touch each other in the same pattern as the Desargues configuration. Extend each of the edges of the 5-cell to the line that contains it (its affine hull), similarly extend each triangle of the 5-cell to the 2-dimensional plane that contains it, and intersect these lines and planes by a three-dimensional hyperplane that neither contains nor is parallel to any of them. Each line intersects the hyperplane in a point, and each plane intersects the hyperplane in a line; these ten points and lines form an instance of the Desargues configuration.[2]
Symmetries edit
Although Desargues' theorem chooses different roles for its ten lines and points, the Desargues configuration itself is more symmetric: any of the ten points may be chosen to be the center of perspectivity, and that choice determines which six points will be the vertices of triangles and which line will be the axis of perspectivity. The Desargues configuration has a symmetry group of order 120; that is, there are 120 different ways of permuting the points and lines of the configuration in a way that preserves its point-line incidences.[3] The three-dimensional construction of the Desargues configuration makes these symmetries more readily apparent: if the configuration is generated from five planes in general position in three dimensions, then each of the 120 different permutations of these five planes corresponds to a symmetry of the configuration.[2]
The Desargues configuration is self-dual, meaning that it is possible to find a correspondence from points of one Desargues configuration to lines of a second configuration, and from lines of the first configuration to points of a second configuration, in such a way that all of the configuration's incidences are preserved.[4]
Graphs edit
The Levi graph of the Desargues configuration, a graph having one vertex for each point or line in the configuration, is known as the Desargues graph. Because of the symmetries and self-duality of the Desargues configuration, the Desargues graph is a symmetric graph.[1]
Kempe (1886) draws a different graph for this configuration, with ten vertices representing its ten lines, and with two vertices connected by an edge whenever the corresponding two lines do not meet at one of the points of the configuration. Alternatively, the vertices of this graph may be interpreted as representing the points of the Desargues configuration, in which case the edges connect pairs of points for which the line connecting them is not part of the configuration. This publication marks the first known appearance of the Petersen graph in the mathematical literature, 12 years before Julius Petersen's use of the same graph as a counterexample to an edge coloring problem.[5]
Related configurations edit
As a projective configuration, the Desargues configuration has the notation (103103), meaning that each of its ten points is incident to three lines and each of its ten lines is incident to three points. Its ten points can be viewed in a unique way as a pair of mutually inscribed pentagons, or as a self-inscribed decagon.[6] The Desargues graph, a 20-vertex bipartite symmetric cubic graph, is so called because it can be interpreted as the Levi graph of the Desargues configuration, with a vertex for each point and line of the configuration and an edge for every incident point-line pair.[1]
There also exist eight other (103103) configurations (that is, sets of points and lines in the Euclidean plane with three lines per point and three points per line) that are not incidence-isomorphic to the Desargues configuration, one of which is shown at right. A tenth configuration exists as an abstract finite geometry but cannot be realized using Euclidean points and lines.[7] In all of these configurations, each point has three other points that are not collinear with it. But in the Desargues configuration, these three points are always collinear with each other (if the chosen point is the center of perspectivity, then the three points form the axis of perspectivity) while in the other configuration shown in the illustration these three points form a triangle of three lines. As with the Desargues configuration, the other depicted configuration can be viewed as a pair of mutually inscribed pentagons.[8]
Notes edit
- ^ a b c Pisanski & Servatius (2013).
- ^ a b c d Barnes (2012).
- ^ Stroppel & Stroppel (2013).
- ^ Coxeter (1964).
- ^ Holton & Sheehan (1993).
- ^ Hilbert & Cohn-Vossen (1952), pp. 125–127.
- ^ Schroeter (1889); Hilbert & Cohn-Vossen (1952, pp. 127–128)
- ^ This configuration is the cyclic 103 configuration, part of a family of configurations studied by Berman et al. (2020).
References edit
- Barnes, John (2012), "Duality in three dimensions", Gems of Geometry, Springer, pp. 95–97, ISBN 9783642309649
- Berman, Leah Wrenn; DeOrsey, Philip; Faudree, Jill R.; Pisanski, Tomaž; Žitnik, Arjana (2020), "Chiral astral realizations of cyclic 3-configurations", Discrete & Computational Geometry, 64 (2): 542–565, doi:10.1007/s00454-020-00203-1, MR 4131561
- Coxeter, H.S.M. (1964), Projective Geometry, New York: Blaisdell, pp. 26–27
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, pp. 119–128, ISBN 0-8284-1087-9
- Holton, D. A.; Sheehan, J. (1993), The Petersen Graph, Australian Mathematical Society Lecture Series, vol. 7, Cambridge University Press, Cambridge, p. 1, doi:10.1017/CBO9780511662058, ISBN 0-521-43594-3, MR 1232658
- Kempe, A. B. (1886), "A memoir on the theory of mathematical form", Philosophical Transactions of the Royal Society of London, 177: 1–70, doi:10.1098/rstl.1886.0002
- Pisanski, Tomaž; Servatius, Brigitte (2013), "5.3.4 The Desargues configuration", Configurations from a Graphical Viewpoint, Springer, pp. 176–179, ISBN 9780817683641
- Schroeter, H. (1889), "Ueber die Bildungsweise und geometrische Konstruction der Konfigurationen 103", Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen, 1889: 193–236
- Stroppel, Bernhild; Stroppel, Markus (2013), "Desargues, doily, dualities and exceptional isomorphisms" (PDF), Australasian Journal of Combinatorics, 57: 257