In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so "quadratic polynomial" and "quadratic function" were almost synonymous. This is still the case in many elementary courses, where both terms are often abbreviated as "quadratic".
For example, a univariate (single-variable) quadratic function has the form[1]
where x is its variable. The graph of a univariate quadratic function is a parabola, a curve that has an axis of symmetry parallel to the y-axis.
If a quadratic function is equated with zero, then the result is a quadratic equation. The solutions of a quadratic equation are the zeros of the corresponding quadratic function.
The bivariate case in terms of variables x and y has the form
with at least one of a, b, c not equal to zero. The zeros of this quadratic function is, in general (that is, if a certain expression of the coefficients is not equal to zero), a conic section (a circle or other ellipse, a parabola, or a hyperbola).
A quadratic function in three variables x, y, and z contains exclusively terms x2, y2, z2, xy, xz, yz, x, y, z, and a constant:
where at least one of the coefficients a, b, c, d, e, f of the second-degree terms is not zero.
A quadratic function can have an arbitrarily large number of variables. The set of its zero form a quadric, which is a surface in the case of three variables and a hypersurface in general case.
Etymology edit
The adjective quadratic comes from the Latin word quadrātum ("square"). A term raised to the second power like x2 is called a square in algebra because it is the area of a square with side x.
Terminology edit
Coefficients edit
The coefficients of a quadratic function are often taken to be real or complex numbers, but they may be taken in any ring, in which case the domain and the codomain are this ring (see polynomial evaluation).
Degree edit
When using the term "quadratic polynomial", authors sometimes mean "having degree exactly 2", and sometimes "having degree at most 2". If the degree is less than 2, this may be called a "degenerate case". Usually the context will establish which of the two is meant.
Sometimes the word "order" is used with the meaning of "degree", e.g. a second-order polynomial. However, where the "degree of a polynomial" refers to the largest degree of a non-zero term of the polynomial, more typically "order" refers to the lowest degree of a non-zero term of a power series.
Variables edit
A quadratic polynomial may involve a single variable x (the univariate case), or multiple variables such as x, y, and z (the multivariate case).
The one-variable case edit
Any single-variable quadratic polynomial may be written as
where x is the variable, and a, b, and c represent the coefficients. Such polynomials often arise in a quadratic equation The solutions to this equation are called the roots and can be expressed in terms of the coefficients as the quadratic formula. Each quadratic polynomial has an associated quadratic function, whose graph is a parabola.
Bivariate and multivariate cases edit
Any quadratic polynomial with two variables may be written as
where x and y are the variables and a, b, c, d, e, f are the coefficients, and one of a, b and c is nonzero. Such polynomials are fundamental to the study of conic sections, as the implicit equation of a conic section is obtained by equating to zero a quadratic polynomial, and the zeros of a quadratic function form a (possibly degenerate) conic section.
Similarly, quadratic polynomials with three or more variables correspond to quadric surfaces or hypersurfaces.
Quadratic polynomials that have only terms of degree two are called quadratic forms.
Forms of a univariate quadratic function edit
A univariate quadratic function can be expressed in three formats:[2]
- is called the standard form,
- is called the factored form, where r1 and r2 are the roots of the quadratic function and the solutions of the corresponding quadratic equation.
- is called the vertex form, where h and k are the x and y coordinates of the vertex, respectively.
The coefficient a is the same value in all three forms. To convert the standard form to factored form, one needs only the quadratic formula to determine the two roots r1 and r2. To convert the standard form to vertex form, one needs a process called completing the square. To convert the factored form (or vertex form) to standard form, one needs to multiply, expand and/or distribute the factors.
Graph of the univariate function edit
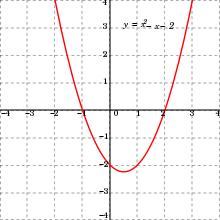
Regardless of the format, the graph of a univariate quadratic function is a parabola (as shown at the right). Equivalently, this is the graph of the bivariate quadratic equation .
- If a > 0, the parabola opens upwards.
- If a < 0, the parabola opens downwards.
The coefficient a controls the degree of curvature of the graph; a larger magnitude of a gives the graph a more closed (sharply curved) appearance.
The coefficients b and a together control the location of the axis of symmetry of the parabola (also the x-coordinate of the vertex and the h parameter in the vertex form) which is at
The coefficient c controls the height of the parabola; more specifically, it is the height of the parabola where it intercepts the y-axis.
Vertex edit
The vertex of a parabola is the place where it turns; hence, it is also called the turning point. If the quadratic function is in vertex form, the vertex is (h, k). Using the method of completing the square, one can turn the standard form
into
so the vertex, (h, k), of the parabola in standard form is
If the quadratic function is in factored form
the average of the two roots, i.e.,
is the x-coordinate of the vertex, and hence the vertex (h, k) is
The vertex is also the maximum point if a < 0, or the minimum point if a > 0.
The vertical line
that passes through the vertex is also the axis of symmetry of the parabola.
Maximum and minimum points edit
Using calculus, the vertex point, being a maximum or minimum of the function, can be obtained by finding the roots of the derivative:
x is a root of f '(x) if f '(x) = 0 resulting in
with the corresponding function value
so again the vertex point coordinates, (h, k), can be expressed as
Roots of the univariate function edit
- Roots and y-intercept in red
- Vertex and axis of symmetry in blue
- Focus and directrix in pink
Exact roots edit
The roots (or zeros), r1 and r2, of the univariate quadratic function
are the values of x for which f(x) = 0.
When the coefficients a, b, and c, are real or complex, the roots are
Upper bound on the magnitude of the roots edit
The modulus of the roots of a quadratic can be no greater than where is the golden ratio [4][importance?]
The square root of a univariate quadratic function edit
The square root of a univariate quadratic function gives rise to one of the four conic sections, almost always either to an ellipse or to a hyperbola.
If then the equation describes a hyperbola, as can be seen by squaring both sides. The directions of the axes of the hyperbola are determined by the ordinate of the minimum point of the corresponding parabola If the ordinate is negative, then the hyperbola's major axis (through its vertices) is horizontal, while if the ordinate is positive then the hyperbola's major axis is vertical.
If then the equation describes either a circle or other ellipse or nothing at all. If the ordinate of the maximum point of the corresponding parabola is positive, then its square root describes an ellipse, but if the ordinate is negative then it describes an empty locus of points.
Iteration edit
To iterate a function , one applies the function repeatedly, using the output from one iteration as the input to the next.
One cannot always deduce the analytic form of , which means the nth iteration of . (The superscript can be extended to negative numbers, referring to the iteration of the inverse of if the inverse exists.) But there are some analytically tractable cases.
For example, for the iterative equation
one has
where
- and
So by induction,
can be obtained, where can be easily computed as
Finally, we have
as the solution.
See Topological conjugacy for more detail about the relationship between f and g. And see Complex quadratic polynomial for the chaotic behavior in the general iteration.
The logistic map
with parameter 2<r<4 can be solved in certain cases, one of which is chaotic and one of which is not. In the chaotic case r=4 the solution is
where the initial condition parameter is given by . For rational , after a finite number of iterations maps into a periodic sequence. But almost all are irrational, and, for irrational , never repeats itself – it is non-periodic and exhibits sensitive dependence on initial conditions, so it is said to be chaotic.
The solution of the logistic map when r=2 is
for . Since for any value of other than the unstable fixed point 0, the term goes to 0 as n goes to infinity, so goes to the stable fixed point
Bivariate (two variable) quadratic function edit
A bivariate quadratic function is a second-degree polynomial of the form
where A, B, C, D, and E are fixed coefficients and F is the constant term. Such a function describes a quadratic surface. Setting equal to zero describes the intersection of the surface with the plane which is a locus of points equivalent to a conic section.
Minimum/maximum edit
If the function has no maximum or minimum; its graph forms a hyperbolic paraboloid.
If the function has a minimum if both A > 0 and B > 0, and a maximum if both A < 0 and B < 0; its graph forms an elliptic paraboloid. In this case the minimum or maximum occurs at where:
If and the function has no maximum or minimum; its graph forms a parabolic cylinder.
If and the function achieves the maximum/minimum at a line—a minimum if A>0 and a maximum if A<0; its graph forms a parabolic cylinder.
See also edit
References edit
- ^ "Quadratic Equation from Wolfram MathWorld". Retrieved January 6, 2013.
- ^ Hughes-Hallett, Deborah; Connally, Eric; McCallum, William G. (2007), College Algebra, John Wiley & Sons Inc., p. 205, ISBN 9780471271758
- ^ "Complex Roots Made Visible – Math Fun Facts". Retrieved 1 October 2016.
- ^ Lord, Nick, "Golden bounds for the roots of quadratic equations", Mathematical Gazette 91, November 2007, 549.
- Algebra 1, Glencoe, ISBN 0-07-825083-8
- Algebra 2, Saxon, ISBN 0-939798-62-X


