This article needs additional citations for verification. (August 2017) |
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably".[1] An overfitted model is a mathematical model that contains more parameters than can be justified by the data.[2] In a mathematical sense, these parameters represent the degree of a polynomial. The essence of overfitting is to have unknowingly extracted some of the residual variation (i.e., the noise) as if that variation represented underlying model structure.[3]: 45


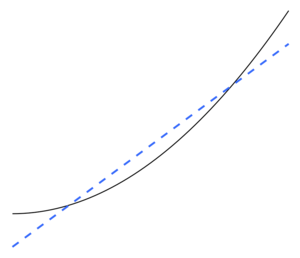
Underfitting occurs when a mathematical model cannot adequately capture the underlying structure of the data. An under-fitted model is a model where some parameters or terms that would appear in a correctly specified model are missing.[2] Under-fitting would occur, for example, when fitting a linear model to non-linear data. Such a model will tend to have poor predictive performance.
The possibility of over-fitting exists because the criterion used for selecting the model is not the same as the criterion used to judge the suitability of a model. For example, a model might be selected by maximizing its performance on some set of training data, and yet its suitability might be determined by its ability to perform well on unseen data; then over-fitting occurs when a model begins to "memorize" training data rather than "learning" to generalize from a trend.
As an extreme example, if the number of parameters is the same as or greater than the number of observations, then a model can perfectly predict the training data simply by memorizing the data in its entirety. (For an illustration, see Figure 2.) Such a model, though, will typically fail severely when making predictions.
Overfitting is directly related to approximation error of the selected function class and the optimization error of the optimization procedure. A function class that is too large, in a suitable sense, relative to the dataset size is likely to overfit.[4] Even when the fitted model does not have an excessive number of parameters, it is to be expected that the fitted relationship will appear to perform less well on a new data set than on the data set used for fitting (a phenomenon sometimes known as shrinkage).[2] In particular, the value of the coefficient of determination will shrink relative to the original data.
To lessen the chance or amount of overfitting, several techniques are available (e.g., model comparison, cross-validation, regularization, early stopping, pruning, Bayesian priors, or dropout). The basis of some techniques is either (1) to explicitly penalize overly complex models or (2) to test the model's ability to generalize by evaluating its performance on a set of data not used for training, which is assumed to approximate the typical unseen data that a model will encounter.
Statistical inference edit
This section needs expansion. You can help by adding to it. (October 2017) |
In statistics, an inference is drawn from a statistical model, which has been selected via some procedure. Burnham & Anderson, in their much-cited text on model selection, argue that to avoid overfitting, we should adhere to the "Principle of Parsimony".[3] The authors also state the following.[3]: 32–33
Overfitted models ... are often free of bias in the parameter estimators, but have estimated (and actual) sampling variances that are needlessly large (the precision of the estimators is poor, relative to what could have been accomplished with a more parsimonious model). False treatment effects tend to be identified, and false variables are included with overfitted models. ... A best approximating model is achieved by properly balancing the errors of underfitting and overfitting.
Overfitting is more likely to be a serious concern when there is little theory available to guide the analysis, in part because then there tend to be a large number of models to select from. The book Model Selection and Model Averaging (2008) puts it this way.[5]
Given a data set, you can fit thousands of models at the push of a button, but how do you choose the best? With so many candidate models, overfitting is a real danger. Is the monkey who typed Hamlet actually a good writer?
Regression edit
In regression analysis, overfitting occurs frequently.[6] As an extreme example, if there are p variables in a linear regression with p data points, the fitted line can go exactly through every point.[7] For logistic regression or Cox proportional hazards models, there are a variety of rules of thumb (e.g. 5–9,[8] 10[9] and 10–15[10] — the guideline of 10 observations per independent variable is known as the "one in ten rule"). In the process of regression model selection, the mean squared error of the random regression function can be split into random noise, approximation bias, and variance in the estimate of the regression function. The bias–variance tradeoff is often used to overcome overfit models.
With a large set of explanatory variables that actually have no relation to the dependent variable being predicted, some variables will in general be falsely found to be statistically significant and the researcher may thus retain them in the model, thereby overfitting the model. This is known as Freedman's paradox.
Machine learning edit
Usually a learning algorithm is trained using some set of "training data": exemplary situations for which the desired output is known. The goal is that the algorithm will also perform well on predicting the output when fed "validation data" that was not encountered during its training.
Overfitting is the use of models or procedures that violate Occam's razor, for example by including more adjustable parameters than are ultimately optimal, or by using a more complicated approach than is ultimately optimal. For an example where there are too many adjustable parameters, consider a dataset where training data for y can be adequately predicted by a linear function of two independent variables. Such a function requires only three parameters (the intercept and two slopes). Replacing this simple function with a new, more complex quadratic function, or with a new, more complex linear function on more than two independent variables, carries a risk: Occam's razor implies that any given complex function is a priori less probable than any given simple function. If the new, more complicated function is selected instead of the simple function, and if there was not a large enough gain in training-data fit to offset the complexity increase, then the new complex function "overfits" the data, and the complex overfitted function will likely perform worse than the simpler function on validation data outside the training dataset, even though the complex function performed as well, or perhaps even better, on the training dataset.[11]
When comparing different types of models, complexity cannot be measured solely by counting how many parameters exist in each model; the expressivity of each parameter must be considered as well. For example, it is nontrivial to directly compare the complexity of a neural net (which can track curvilinear relationships) with m parameters to a regression model with n parameters.[11]
Overfitting is especially likely in cases where learning was performed too long or where training examples are rare, causing the learner to adjust to very specific random features of the training data that have no causal relation to the target function. In this process of overfitting, the performance on the training examples still increases while the performance on unseen data becomes worse.
As a simple example, consider a database of retail purchases that includes the item bought, the purchaser, and the date and time of purchase. It's easy to construct a model that will fit the training set perfectly by using the date and time of purchase to predict the other attributes, but this model will not generalize at all to new data, because those past times will never occur again.
Generally, a learning algorithm is said to overfit relative to a simpler one if it is more accurate in fitting known data (hindsight) but less accurate in predicting new data (foresight). One can intuitively understand overfitting from the fact that information from all past experience can be divided into two groups: information that is relevant for the future, and irrelevant information ("noise"). Everything else being equal, the more difficult a criterion is to predict (i.e., the higher its uncertainty), the more noise exists in past information that needs to be ignored. The problem is determining which part to ignore. A learning algorithm that can reduce the risk of fitting noise is called "robust."
Consequences edit
The most obvious consequence of overfitting is poor performance on the validation dataset. Other negative consequences include:
- A function that is overfitted is likely to request more information about each item in the validation dataset than does the optimal function; gathering this additional unneeded data can be expensive or error-prone, especially if each individual piece of information must be gathered by human observation and manual data-entry.[11]
- A more complex, overfitted function is likely to be less portable than a simple one. At one extreme, a one-variable linear regression is so portable that, if necessary, it could even be done by hand. At the other extreme are models that can be reproduced only by exactly duplicating the original modeler's entire setup, making reuse or scientific reproduction difficult.[11]
- It may be possible to reconstruct details of individual training instances from an overfitted machine learning model's training set. This may be undesirable if, for example, the training data includes sensitive personally identifiable information (PII). This phenomenon also presents problems in the area of artificial intelligence and copyright, with the developers of some generative deep learning models such as Stable Diffusion and GitHub Copilot being sued for copyright infringement because these models have been found to be capable of reproducing certain copyrighted items from their training data.[12][13]
Remedy edit
The optimal function usually needs verification on bigger or completely new datasets. There are, however, methods like minimum spanning tree or life-time of correlation that applies the dependence between correlation coefficients and time-series (window width). Whenever the window width is big enough, the correlation coefficients are stable and don't depend on the window width size anymore. Therefore, a correlation matrix can be created by calculating a coefficient of correlation between investigated variables. This matrix can be represented topologically as a complex network where direct and indirect influences between variables are visualized. Dropout regularisation can also improve robustness and therefore reduce over-fitting by probabilistically removing inputs to a layer.
Underfitting edit
Underfitting is the inverse of overfitting, meaning that the statistical model or machine learning algorithm is too simplistic to accurately capture the patterns in the data. A sign of underfitting is that there is a high bias and low variance detected in the current model or algorithm used (the inverse of overfitting: low bias and high variance). This can be gathered from the Bias-variance tradeoff which is the method of analyzing a model or algorithm for bias error, variance error and irreducible error. With a high bias and low variance the result of the model is that it will inaccurately represent the data points and thus insufficiently be able to predict future data results (see Generalization error). Shown in Figure 5 the linear line could not represent all the given data points due to the line not resembling the curvature of the points. We would expect to see a parabola shaped line as shown in Figure 6 and Figure 1. As previously mentioned if we were to use Figure 5 for analysis we would get false predictive results contrary to the results if we analyzed Figure 6.
Burnham & Anderson state the following.[3]: 32
... an underfitted model would ignore some important replicable (i.e., conceptually replicable in most other samples) structure in the data and thus fail to identify effects that were actually supported by the data. In this case, bias in the parameter estimators is often substantial, and the sampling variance is underestimated, both factors resulting in poor confidence interval coverage. Underfitted models tend to miss important treatment effects in experimental settings.
Resolving underfitting edit
There are multiple ways to deal with underfitting:
- Increase the complexity of the model: If the model is too simple, it may be necessary to increase its complexity by adding more features, increasing the number of parameters, or using a more flexible model. However, this should be done carefully to avoid overfitting.[14]
- Use a different algorithm: If the current algorithm is not able to capture the patterns in the data, it may be necessary to try a different one. For example, a neural network may be more effective than a linear regression model for some types of data.[14]
- Increase the amount of training data: If the model is underfitting due to lack of data, increasing the amount of training data may help. This will allow the model to better capture the underlying patterns in the data.[14]
- Regularization: Regularization is a technique used to prevent overfitting by adding a penalty term to the loss function that discourages large parameter values. It can also be used to prevent underfitting by controlling the complexity of the model.[15]
- Ensemble Methods: Ensemble methods combine multiple models to create a more accurate prediction. This can help to reduce underfitting by allowing multiple models to work together to capture the underlying patterns in the data.[16]
- Feature engineering: Feature engineering involves creating new model features from the existing ones that may be more relevant to the problem at hand. This can help to improve the accuracy of the model and prevent underfitting.[14]
Benign overfitting edit
Benign overfitting describes the phenomenon of a statistical model which seems to generalize well to unseen data, even when it has been fit perfectly on noisy training data (i.e. obtains perfect predictive accuracy on the training set). The phenomenon is of particular interest in deep neural networks, but is studied from a theoretical perspective in the context of much simpler models, such as linear regression. In particular, it has been shown that overparameterization is essential for benign overfitting in this setting. In other words, the number of directions in parameter space that are unimportant for prediction must significantly exceed the sample size.[17]
See also edit
- Bias–variance tradeoff
- Curve fitting
- Data dredging
- Feature selection
- Feature engineering
- Freedman's paradox
- Generalization error
- Goodness of fit
- Life-time of correlation
- Model selection
- Researcher degrees of freedom
- Occam's razor
- Primary model
- Vapnik–Chervonenkis dimension – larger VC dimension implies larger risk of overfitting
Notes edit
- ^ Definition of "overfitting" at OxfordDictionaries.com: this definition is specifically for statistics.
- ^ a b c Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press.
- ^ a b c d Burnham, K. P.; Anderson, D. R. (2002), Model Selection and Multimodel Inference (2nd ed.), Springer-Verlag.
- ^ Bottou, Léon; Bousquet, Olivier (2011-09-30), "The Tradeoffs of Large-Scale Learning", Optimization for Machine Learning, The MIT Press, pp. 351–368, ISBN 978-0-262-29877-3, retrieved 2023-12-08
- ^ Claeskens, G.; Hjort, N.L. (2008), Model Selection and Model Averaging, Cambridge University Press.
- ^ Harrell, F. E. Jr. (2001), Regression Modeling Strategies, Springer.
- ^ Martha K. Smith (2014-06-13). "Overfitting". University of Texas at Austin. Retrieved 2016-07-31.
- ^ Vittinghoff, E.; McCulloch, C. E. (2007). "Relaxing the Rule of Ten Events per Variable in Logistic and Cox Regression". American Journal of Epidemiology. 165 (6): 710–718. doi:10.1093/aje/kwk052. PMID 17182981.
- ^ Draper, Norman R.; Smith, Harry (1998). Applied Regression Analysis (3rd ed.). Wiley. ISBN 978-0471170822.
- ^ Jim Frost (2015-09-03). "The Danger of Overfitting Regression Models". Retrieved 2016-07-31.
- ^ a b c d Hawkins, Douglas M (2004). "The problem of overfitting". Journal of Chemical Information and Modeling. 44 (1): 1–12. doi:10.1021/ci0342472. PMID 14741005. S2CID 12440383.
- ^ a b Lee, Timothy B. (3 April 2023). "Stable Diffusion copyright lawsuits could be a legal earthquake for AI". Ars Technica.
- ^ Vincent, James (2022-11-08). "The lawsuit that could rewrite the rules of AI copyright". The Verge. Retrieved 2022-12-07.
- ^ a b c d "ML | Underfitting and Overfitting". GeeksforGeeks. 2017-11-23. Retrieved 2023-02-27.
- ^ Nusrat, Ismoilov; Jang, Sung-Bong (November 2018). "A Comparison of Regularization Techniques in Deep Neural Networks". Symmetry. 10 (11): 648. Bibcode:2018Symm...10..648N. doi:10.3390/sym10110648. ISSN 2073-8994.
- ^ Fernandez, Javier (2022-06-20). "Introduction to Ensemble Methods in Machine Learning". Medium. Retrieved 2023-02-27.
- ^ Bartlett, P.L., Long, P.M., Lugosi, G., & Tsigler, A. (2019). Benign overfitting in linear regression. Proceedings of the National Academy of Sciences, 117, 30063 - 30070.
References edit
- Leinweber, D. J. (2007). "Stupid data miner tricks". The Journal of Investing. 16: 15–22. doi:10.3905/joi.2007.681820. S2CID 108627390.
- Tetko, I. V.; Livingstone, D. J.; Luik, A. I. (1995). "Neural network studies. 1. Comparison of Overfitting and Overtraining" (PDF). Journal of Chemical Information and Modeling. 35 (5): 826–833. doi:10.1021/ci00027a006.
- Tip 7: Minimize overfitting. Chicco, D. (December 2017). "Ten quick tips for machine learning in computational biology". BioData Mining. 10 (35): 35. doi:10.1186/s13040-017-0155-3. PMC 5721660. PMID 29234465.
Further reading edit
- Christian, Brian; Griffiths, Tom (April 2017), "Chapter 7: Overfitting", Algorithms To Live By: The computer science of human decisions, William Collins, pp. 149–168, ISBN 978-0-00-754799-9
External links edit
- Overfitting: when accuracy measure goes wrong – introductory video tutorial
- The Problem of Overfitting Data – Stony Brook University
- What is "overfitting," exactly? – Andrew Gelman blog
- CSE546: Linear Regression Bias / Variance Tradeoff – University of Washington
- Underfitting and Overfitting in machine learning and how to deal with it !!! – Towards Data Science
- What is Underfitting – IBM