| Cubohemioctahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 10, E = 24 V = 12 (χ = −2) |
| Faces by sides | 6{4}+4{6} |
| Coxeter diagram | |
| Wythoff symbol | 4/3 4 | 3 (double-covering) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U15, C51, W78 |
| Dual polyhedron | Hexahemioctacron |
| Vertex figure |  4.6.4/3.6 |
| Bowers acronym | Cho |
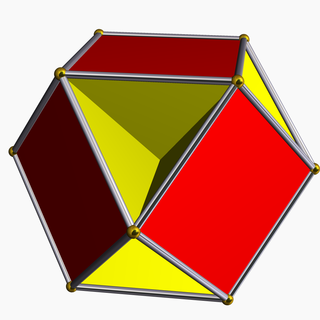
In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. It has 10 faces (6 squares and 4 regular hexagons), 24 edges and 12 vertices.[1] Its vertex figure is a crossed quadrilateral.

It is given Wythoff symbol 4⁄3 4 | 3, although that is a double-covering of this figure.
A nonconvex polyhedron has intersecting faces which do not represent new edges or faces. In the picture vertices are marked by golden spheres, and edges by silver cylinders.
It is a hemipolyhedron with 4 hexagonal faces passing through the model center. The hexagons intersect each other and so only triangular portions of each are visible.
Related polyhedra edit
It shares the vertex arrangement and edge arrangement with the cuboctahedron (having the square faces in common), and with the octahemioctahedron (having the hexagonal faces in common).
| Cuboctahedron |
Cubohemioctahedron |
Octahemioctahedron |
Tetrahexagonal tiling edit
The cubohemioctahedron can be seen as a net on the hyperbolic tetrahexagonal tiling with vertex figure 4.6.4.6.
Hexahemioctacron edit
| Hexahemioctacron | |
|---|---|
| Type | Star polyhedron |
| Face | — |
| Elements | F = 12, E = 24 V = 10 (χ = −2) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU15 |
| dual polyhedron | Cubohemioctahedron |
The hexahemioctacron is the dual of the cubohemioctahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the octahemioctacron.
Since the cubohemioctahedron has four hexagonal faces passing through the model center, thus it is degenerate, and can be seen as having four vertices at infinity.
In Magnus Wenninger's Dual Models, they are represented with intersecting infinite prisms passing through the model center, cut off at a certain point that is convenient for the maker.
See also edit
- Hemi-cube - The four vertices at infinity correspond directionally to the four vertices of this abstract polyhedron.
References edit
- ^ Maeder, Roman. "15: cubohemioctahedron". MathConsult.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (Page 101, Duals of the (nine) hemipolyhedra)
External links edit
- Weisstein, Eric W. "Hexahemioctacron". MathWorld.
- Weisstein, Eric W., "Cubohemioctahedron" ("Uniform polyhedron") at MathWorld.
- Uniform polyhedra and duals