Homothety

In mathematics, a homothety (or homothecy, or homogeneous dilation) is a transformation of an affine space determined by a point S called its center and a nonzero number $k$ called its ratio, which sends point $X$ to a point $X'$ by the rule

Homothety: Example with $k>0$
For $k=1$ one gets the identity (no point is moved),
for $k>1$ an enlargement
for $k<1$ a reduction

Example with $k<0$
For $k=-1$ one gets a point reflection at point $S$

Homothety of a pyramid

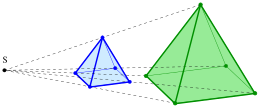
${\overrightarrow {SX'}}=k{\overrightarrow {SX}}$ for a fixed number $k\neq 0$.

Using position vectors:

$\mathbf {x} '=\mathbf {s} +k(\mathbf {x} -\mathbf {s} )$.

In case of $S=O$ (Origin):

$\mathbf {x} '=k\mathbf {x}$,

which is a uniform scaling and shows the meaning of special choices for $k$:

for $k=1$ one gets the identity mapping,

for $k=-1$ one gets the reflection at the center,

For $1/k$ one gets the inverse mapping defined by $k$.

In Euclidean geometry homotheties are the similarities that fix a point and either preserve (if $k>0$) or reverse (if $k<0$) the direction of all vectors. Together with the translations, all homotheties of an affine (or Euclidean) space form a group, the group of dilations or homothety-translations. These are precisely the affine transformations with the property that the image of every line g is a line parallel to g.

In projective geometry, a homothetic transformation is a similarity transformation (i.e., fixes a given elliptic involution) that leaves the line at infinity pointwise invariant.

In Euclidean geometry, a homothety of ratio $k$ multiplies distances between points by $|k|$, areas by $k^{2}$ and volumes by $|k|^{3}$. Here $k$ is the ratio of magnification or dilation factor or scale factor or similitude ratio. Such a transformation can be called an enlargement if the scale factor exceeds 1. The above-mentioned fixed point S is called homothetic center or center of similarity or center of similitude.

The term, coined by French mathematician Michel Chasles, is derived from two Greek elements: the prefix homo- (όμο), meaning "similar", and thesis (Θέσις), meaning "position". It describes the relationship between two figures of the same shape and orientation. For example, two Russian dolls looking in the same direction can be considered homothetic.

Homotheties are used to scale the contents of computer screens; for example, smartphones, notebooks, and laptops.

Properties

The following properties hold in any dimension.

Mapping lines, line segments and angles

A homothety has the following properties:

• A line is mapped onto a parallel line. Hence: angles remain unchanged.
• The ratio of two line segments is preserved.

Both properties show:

• A homothety is a similarity.

Derivation of the properties: In order to make calculations easy it is assumed that the center $S$ is the origin: $\mathbf {x} \to k\mathbf {x}$. A line $g$ with parametric representation $\mathbf {x} =\mathbf {p} +t\mathbf {v}$ is mapped onto the point set $g'$ with equation $\mathbf {x} =k(\mathbf {p} +t\mathbf {v} )=k\mathbf {p} +tk\mathbf {v}$, which is a line parallel to $g$.

The distance of two points $P:\mathbf {p} ,\;Q:\mathbf {q}$ is $|\mathbf {p} -\mathbf {q} |$ and $|k\mathbf {p} -k\mathbf {q} |=|k||\mathbf {p} -\mathbf {q} |$ the distance between their images. Hence, the ratio (quotient) of two line segments remains unchanged .

In case of $S\neq O$ the calculation is analogous but a little extensive.

Consequences: A triangle is mapped on a similar one. The homothetic image of a circle is a circle. The image of an ellipse is a similar one. i.e. the ratio of the two axes is unchanged.

With intercept theorem

Graphical constructions

using the intercept theorem

If for a homothety with center $S$ the image $Q_{1}$ of a point $P_{1}$ is given (see diagram) then the image $Q_{2}$ of a second point $P_{2}$, which lies not on line $SP_{1}$ can be constructed graphically using the intercept theorem: $Q_{2}$ is the common point th two lines ${\overline {P_{1}P_{2}}}$ and ${\overline {SP_{2}}}$. The image of a point collinear with $P_{1},Q_{1}$ can be determined using $P_{2},Q_{2}$.

Pantograph

Geometrical background

Pantograph 3d rendering

using a pantograph

Before computers became ubiquitous, scalings of drawings were done by using a pantograph, a tool similar to a compass.

Construction and geometrical background:

1. Take 4 rods and assemble a mobile parallelogram with vertices $P_{0},Q_{0},H,P$ such that the two rods meeting at $Q_{0}$ are prolonged at the other end as shown in the diagram. Choose the ratio $k$.
2. On the prolonged rods mark the two points $S,Q$ such that $|SQ_{0}|=k|SP_{0}|$ and $|QQ_{0}|=k|HQ_{0}|$. This is the case if $|SQ_{0}|={\tfrac {k}{k-1}}|P_{0}Q_{0}|.$ (Instead of $k$ the location of the center $S$ can be prescribed. In this case the ratio is $k=|SQ_{0}|/|SP_{0}|$.)
3. Attach the mobile rods rotatable at point $S$.
4. Vary the location of point $P$ and mark at each time point $Q$.

Because of $|SQ_{0}|/|SP_{0}|=|Q_{0}Q|/|PP_{0}|$ (see diagram) one gets from the intercept theorem that the points $S,P,Q$ are collinear (lie on a line) and equation $|SQ|=k|SP|$ holds. That shows: the mapping $P\to Q$ is a homothety with center $S$ and ratio $k$.

Composition

The composition of two homotheties with centers $S_{1},S_{2}$ and ratios $k_{1}=2,k_{2}=0{.}3$ mapping $P_{i}\to Q_{i}\to R_{i}$ is a homothety again with its center $S_{3}$ on line ${\overline {S_{1}S_{2}}}$ with ratio $k\cdot l=0{.}6$.

• The composition of two homotheties with the same center $S$ is again a homothety with center $S$. The homotheties with center $S$ form a group.
• The composition of two homotheties with different centers $S_{1},S_{2}$ and its ratios $k_{1},k_{2}$ is

in case of $k_{1}k_{2}\neq 1$ a homothety with its center on line ${\overline {S_{1}S_{2}}}$ and ratio $k_{1}k_{2}$ or

in case of $k_{1}k_{2}=1$ a translation in direction ${\overrightarrow {S_{1}S_{2}}}$. Especially, if $k_{1}=k_{2}=-1$ (point reflections).

Derivation:

For the composition $\sigma _{2}\sigma _{1}$ of the two homotheties $\sigma _{1},\sigma _{2}$ with centers $S_{1},S_{2}$ with

$\sigma _{1}:\mathbf {x} \to \mathbf {s} _{1}+k_{1}(\mathbf {x} -\mathbf {s} _{1}),$

$\sigma _{2}:\mathbf {x} \to \mathbf {s} _{2}+k_{2}(\mathbf {x} -\mathbf {s} _{2})\$

one gets by calculation for the image of point $X:\mathbf {x}$:

$(\sigma _{2}\sigma _{1})(\mathbf {x} )=\mathbf {s} _{2}+k_{2}{\big (}\mathbf {s} _{1}+k_{1}(\mathbf {x} -\mathbf {s} _{1})-\mathbf {s} _{2}{\big )}$

$\qquad \qquad \ =(1-k_{1})k_{2}\mathbf {s} _{1}+(1-k_{2})\mathbf {s} _{2}+k_{1}k_{2}\mathbf {x}$.

Hence, the composition is

in case of $k_{1}k_{2}=1$ a translation in direction ${\overrightarrow {S_{1}S_{2}}}$ by vector $\ (1-k_{2})(\mathbf {s} _{2}-\mathbf {s} _{1})$.

in case of $k_{1}k_{2}\neq 1$ point

$S_{3}:\mathbf {s} _{3}={\frac {(1-k_{1})k_{2}\mathbf {s} _{1}+(1-k_{2})\mathbf {s} _{2}}{1-k_{1}k_{2}}}=\mathbf {s} _{1}+{\frac {1-k_{2}}{1-k_{1}k_{2}}}(\mathbf {s} _{2}-\mathbf {s} _{1})$

is a fixpoint (is not moved) and the composition

$\sigma _{2}\sigma _{1}:\ \mathbf {x} \to \mathbf {s} _{3}+k_{1}k_{2}(\mathbf {x} -\mathbf {s} _{3})\quad$.

is a homothety with center $S_{3}$ and ratio $k_{1}k_{2}$. $S_{3}$ lies on line ${\overline {S_{1}S_{2}}}$.

Composition with a translation

• The composition of a homothety and a translation is a homothety.

Derivation:

The composition of the homothety

$\sigma :\mathbf {x} \to \mathbf {s} +k(\mathbf {x} -\mathbf {s} ),\;k\neq 1,\;$ and the translation

$\tau :\mathbf {x} \to \mathbf {x} +\mathbf {v}$ is

$\tau \sigma :\mathbf {x} \to \mathbf {s} +\mathbf {v} +k(\mathbf {x} -\mathbf {s} )$

$=\mathbf {s} +{\frac {\mathbf {v} }{1-k}}+k\left(\mathbf {x} -(\mathbf {s} +{\frac {\mathbf {v} }{1-k}})\right)$

which is a homothety with center $\mathbf {s} '=\mathbf {s} +{\frac {\mathbf {v} }{1-k}}$ and ratio $k$.

In homogenous coordinates

The homothety $\sigma :\mathbf {x} \to \mathbf {s} +k(\mathbf {x} -\mathbf {s} )$ with center $S=(u,v)$ can be written as the composition of a homothety with center $O$ and a translation:

$\mathbf {x} \to k\mathbf {x} +(1-k)\mathbf {s}$.

Hence $\sigma$ can be represented in homogeneous coordinates by the matrix:

${\begin{pmatrix}k&0&(1-k)u\\0&k&(1-k)v\\0&0&1\end{pmatrix}}$

A pure homothety linear transformation is also conformal because it is composed of translation and uniform scale.

See also

• Scaling (geometry) a similar notion in vector spaces
• Homothetic center, the center of a homothetic transformation taking one of a pair of shapes into the other
• The Hadwiger conjecture on the number of strictly smaller homothetic copies of a convex body that may be needed to cover it
• Homothetic function (economics), a function of the form f(U(y)) in which U is a homogeneous function and f is a monotonically increasing function.

References

• H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961), p. 94
• Hadamard, J., Lessons in Plane Geometry
• Meserve, Bruce E. (1955), "Homothetic transformations", Fundamental Concepts of Geometry, Addison-Wesley, pp. 166–169
• Tuller, Annita (1967), A Modern Introduction to Geometries, University Series in Undergraduate Mathematics, Princeton, NJ: D. Van Nostrand Co.

External links

• Homothety, interactive applet from Cut-the-Knot.